Over the past 6 months I have been selected to participate in a MOOC event held by the Imperial team. This is a course consisting of online video lessons, virtual mentors and in-person lectures at Imperial primarily designed to assist the learning of AS further mathematics. It introduced challenging concepts that goes above and beyond the curriculum which consolidated my interest in pursuing a future degree in mathematics.

Immediately after hearing about this from my maths teacher, I was hooked on the idea. Mathematics have always been a lonely journey and the thought of having the privelege to work in groups with the aid of a personalised mentor from the Imperial team was very exciting.

I sent an application form, I put a lot of effort into crafting my application knowing that the spaces onto the course is very limited and very competitive. After waiting a month or so, I received the confirmation letter. Soon, I was on my merry way riding the train to imperial campus.

Course 1

After a nearly 3 hour trek, I finally arrived at Imperial’s Royal School of Mines building. We started off the day with an introductory session on Moser’s circle problem. This was something that I’ve came across briefly, so it was very rewarding getting a full explanation of the mathematics and topology behind Moser’s circle problem.

Moser’s circle problem is about placing n number of points on the circumference of a circle, connecting two of them to form a chord and seeing how many regions are formed with n points. First we were introduced to the idea of planar graphs, which I believe is a collection of non-intersecting vertices and nodes in space. All planar graphs satisfy the formula V-E+F = 2 (with V being the vertices, E being edges and F being the number of regions).

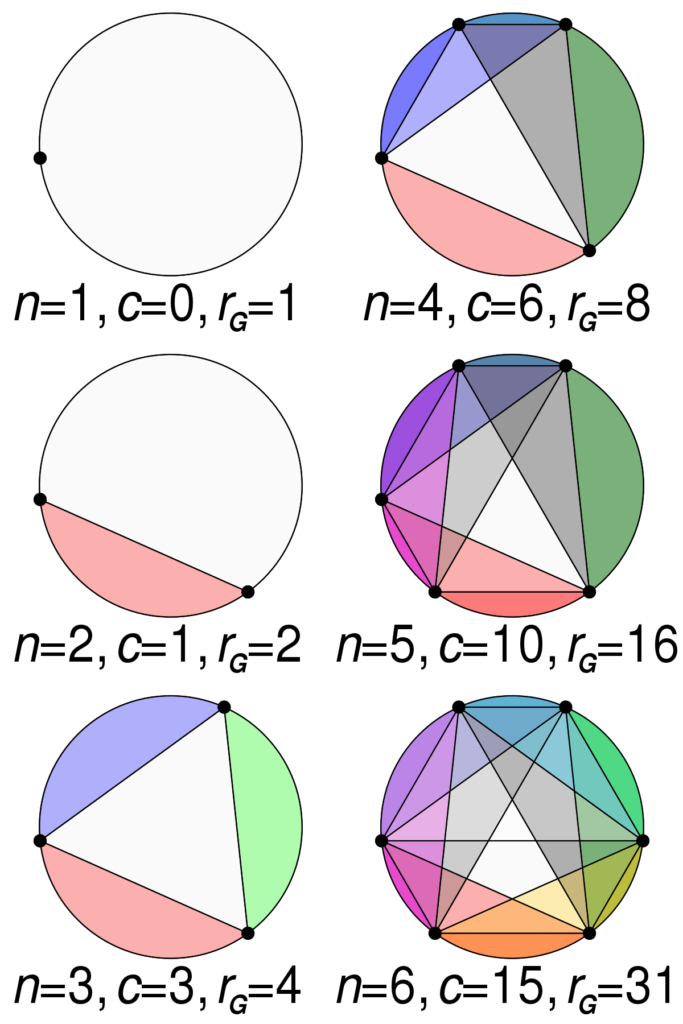
Since the shape formed from Moser’s circle problem is intersecting, it is not exactly a planar graph. But we can chop up the edge at every intersection to turn the shape into a planar graph

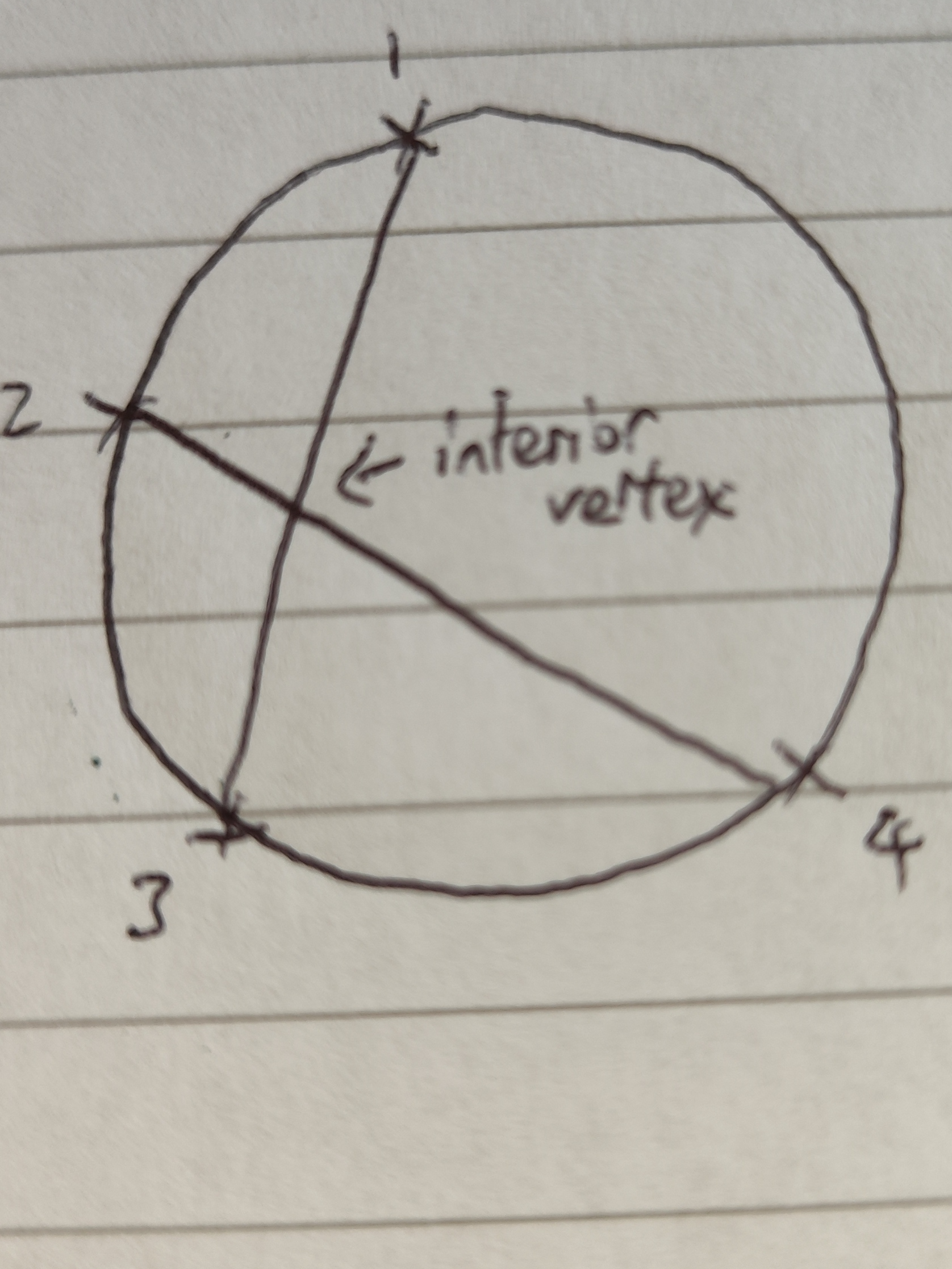
Edges: On the circumference there are n edges (the line connecting two points on the circumference yields one edge). Originally, two points joined together forms a chord (an edge) yielding nC2 edges, however, we had to chop up each intersection to form a planar graph. Before, every intersection point is consisted of two edges, but after chopping it up, every intersection yields an extra two edges, yielding an extra 2 x nC4 edges. Thus the total number of edges is (nC2 + 2 x nC4 + n)

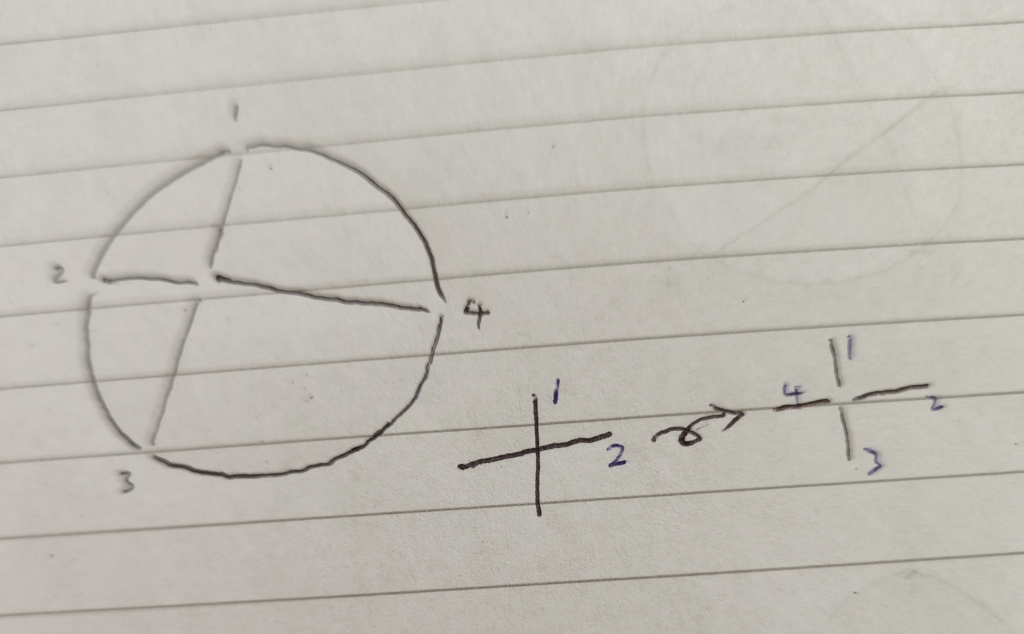
Faces (regions): Using euler’s characteristic formula for planar graphs, F = E – V + 2, excluding the entire exterior region, F = E – V + 1.

F = (nC2 + 2 x nC4 + n) – (n + nC4) + 1

simplifying we get: F = nC2 + nC4 + 1

Using this formula we get the number of regions for 1, 2, 3, 4, 5, 6 vertices being 1, 2, 4, 8, 16, 31

This was an interesting but also a brainfucking start to the day.

After the introductionary lecture, we had an icebreaker session which was interesting. Then we started a lecture on complex numbers. The lecture room was set up really nicely, with a giant projector at the front of the hall, and smaller projectors dotted around for those sitting at the back to see with ease. It felt like we were about tho enjoy a show more than a maths lecture in all honestly. Having not covered anything in the further maths course, the complex number lecture was something new. A topic I’ve never came across before at that time. So learning about it was exciting.

The second lecture was focused on matrices, invariant points and lines and all that. It was a bit boring ngl it wasn’t even hard, at that point I was pretty mentally depleted and wanted to go home.

Then I went home! (surprise surprise)